Linear transformations particularity of DirectXMath library

Computer graphics in Game development

Ivan Belyavtsev

7.04.2020

Transformation issues

Expected image

Current image

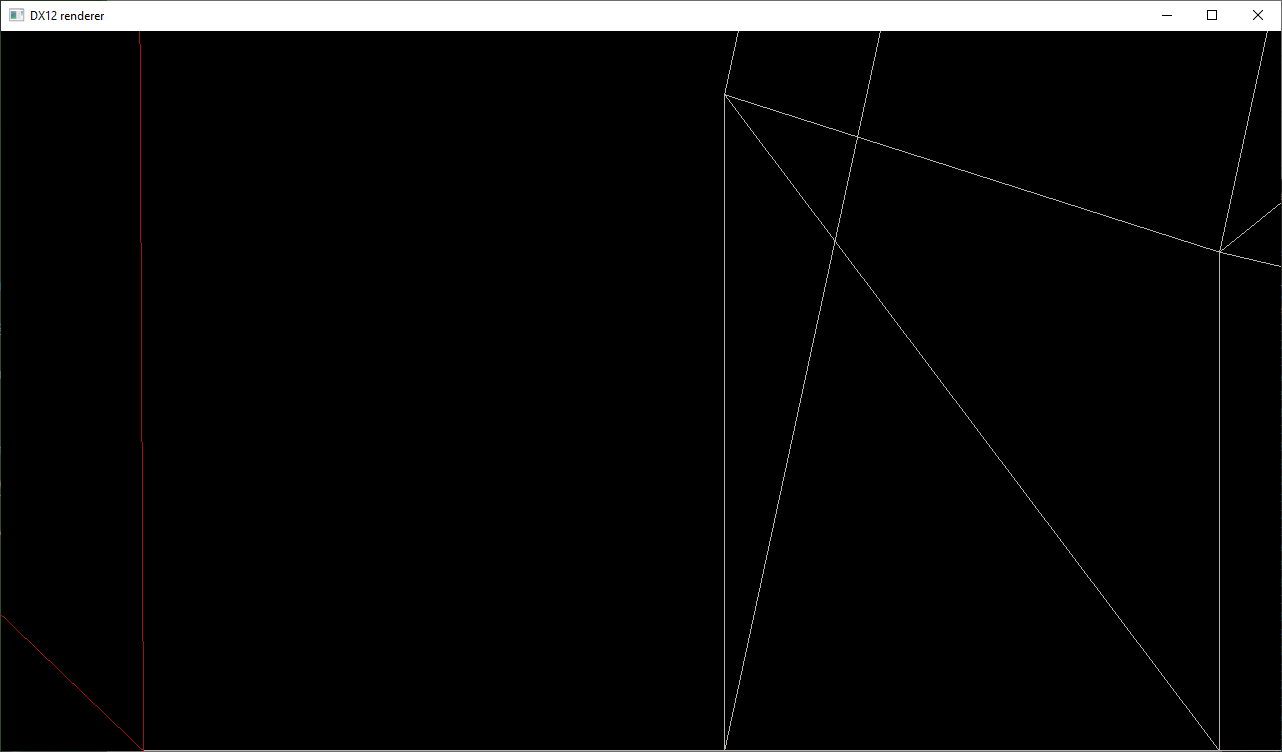
Math background

Linear transformation

\[\mathbf{A} : V \to W\] \[\vec{y}=\mathbf{A}\vec{x}\]

[1]

Matrix

\[ \mathbf{A}=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \]

[1]

Matrix multiplication

\(\mathbf{A}\) is a \((m \times n)\) matrix

\(\mathbf{B}\) is a \((n \times k)\) matrix

\(\mathbf{C}\) is a \((m \times k)\) matrix

\[\mathbf{C} = \mathbf{A}\mathbf{B}\]p

\[c_{ij}=\sum^{n}_{l=1}a_{il}b_{lj}\]

[1]

Matrix multiplication properties

• Non-commutativity: \(\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}\)
• Associativity: \((\mathbf{A}\mathbf{B})\mathbf{C} = \mathbf{A}(\mathbf{B}\mathbf{C})\)
• Transpose commutativity: \((\mathbf{A}\mathbf{B})^T = \mathbf{B}^T\mathbf{A}^T\) [1]

Required linear transformation

\[\vec{y}=(\mathbf{P}\mathbf{V}\mathbf{W})\vec{x}\]

Test case №1

\[\left( \begin{smallmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12\\ 13 & 14 & 15 & 16 \end{smallmatrix} \right) \left( \begin{smallmatrix} 16 & 15 & 14 & 13\\ 12 & 11 & 10 & 9\\ 8 & 7 & 6 & 5\\ 4 & 3 & 2 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix} 80 & 70 & 60 & 50 \\ 240 & 214 & 188 & 162 \\ 400 & 358 & 316 & 274 \\ 560 & 502 & 444 & 386 \end{smallmatrix} \right) \]

Test case №2

\[\left( \begin{smallmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12\\ 13 & 14 & 15 & 16 \end{smallmatrix} \right) \left( \begin{smallmatrix} 1 \\ 2 \\ 3 \\ 4 \end{smallmatrix} \right) = \left( \begin{smallmatrix} 30 \\ 70 \\ 110 \\ 150 \end{smallmatrix} \right) \]

Test for libraries

• Libraries in test: linalg, DirectXMath
• Testing framework: catch2
• Code snippet: Linalg and DirectXMath comparison

Linear transformations in Linalg

Matrix order

Linalg has column-major order [2]

float4x4 A = { {1, 5, 9, 13}, {2, 6, 10, 14},
               {3, 7, 11, 15}, {4, 8, 12, 16} };
float4x4 B = { {16, 12, 8, 4 }, {15, 11, 7, 3 },
               {14, 10, 6, 2}, {13, 9, 5, 1} };
float4x4 ExpectedMatrix = {
               { 80, 240, 400, 560 },
               { 70, 214, 358, 502 },
               { 60, 188, 316, 444 },
               { 50, 162, 274, 386 } };

Non-commutativity

REQUIRE(mul(A, B) != (A * B));
REQUIRE(mul(A, B) == ExpectedMatrix);
REQUIRE(mul(B, A) != ExpectedMatrix);

Transpose commutativity

REQUIRE(mul(transpose(B), transpose(A)) == transpose(mul(A, B)));
REQUIRE(transpose(mul(transpose(B), transpose(A))) == ExpectedMatrix);

Linear transformation

float4x4 A = { {1, 5, 9, 13}, {2, 6, 10, 14},
               {3, 7, 11, 15}, {4, 8, 12, 16} };
float4 X = { 1, 2, 3, 4 };
float4 ExpectedVector = { 30, 70, 110, 150 };

REQUIRE(mul(A, X) == ExpectedVector);

Linear transformations in DirectXMath

Matrix order

DirecXMath has row-major order [3]

XMMATRIX A (1.f, 2.f, 3.f, 4.f, 5.f, 6.f, 7.f, 8.f,
            9.f, 10., 11.f, 12.f, 13.f, 14.f, 15.f, 16.f);
XMMATRIX B (16.f, 15.f, 14.f, 13.f, 12.f, 11.f, 10.f, 9.f,
            8.f, 7.f, 6.f, 5.f, 4.f, 3.f, 2.f, 1.f);
XMMATRIX ExpectedMatrix (80.f, 70.f, 60.f, 50.f,
                         240.f, 214.f, 188.f, 162.f,
                         400.f, 358.f, 316.f, 274.f,
                         560.f, 502.f, 444.f, 386.f);

Non-commutativity

REQUIRE(IsXMMATRIXAreEqual(XMMatrixMultiply(A, B), (A * B)));
REQUIRE(IsXMMATRIXAreEqual(ExpectedMatrix, (A * B)));
REQUIRE(!IsXMMATRIXAreEqual(ExpectedMatrix, (B * A)));

Transpose commutativity

REQUIRE(IsXMMATRIXAreEqual(
    ExpectedMatrix,
    XMMatrixTranspose(XMMatrixTranspose(B) * XMMatrixTranspose(A))));
REQUIRE(IsXMMATRIXAreEqual(
    XMMatrixTranspose(A * B),
    XMMatrixTranspose(B) * XMMatrixTranspose(A)));

Linear transformation

XMFLOAT4 X(1.f, 2.f, 3.f, 4.f);
XMFLOAT4 ExpectedVector(30.f, 70.f, 110.f, 150.f);

REQUIRE(XMVector4Equal(
    XMVector4Transform(XMLoadFloat4(&X), XMMatrixTranspose(A)),
    XMLoadFloat4(&ExpectedVector)));

Linear transformations in HLSL

Matrix order

Default order is column-major [4]

Possible to change to row-major using the next pragma:

#pragma pack_matrix( row_major )

Linear transformation

Order of mul arguments defines layout of vector [4]

//X is a row vector
float4 ExpectedVector = mul(X, A);
//X is a column vector
float4 ExpectedVector = mul(A, X);

How to fix the issue

Row-major style

\[\vec{y}=\vec{x}(\mathbf{W}\mathbf{V}\mathbf{P})\]

world_view_projection = world * view * projection;

#pragma pack_matrix( row_major )
...
result.position = mul(position, mwpMatrix);

Column-major style

\[\vec{y}=(\mathbf{P}^T\mathbf{V}^T\mathbf{W}^T)^T\vec{x}\]

world_view_projection = XMMatrixTranspose(projection) *
                        XMMatrixTranspose(view) *
                        XMMatrixTranspose(world);

#pragma pack_matrix( row_major )
...
result.position = mul(mwpMatrix, position);

Mixed style

\[\vec{y}=(\mathbf{W}\mathbf{V}\mathbf{P})^T\vec{x}\]

world_view_projection = world * view * projection;

result.position = mul(mwpMatrix, position);

DirectX samples style

\[\vec{y}=(\mathbf{P}^T\mathbf{V}^T\mathbf{W}^T)^T\vec{x}\]

world_view_projection = XMMatrixTranspose(
                        XMMatrixTranspose(projection) *
                        XMMatrixTranspose(view) *
                        XMMatrixTranspose(world));

result.position = mul(mwpMatrix, position);

References