Lecture #4: Triangle rasterization

Rasterization

• We have a wire frame image
• Need to fill triangles by color

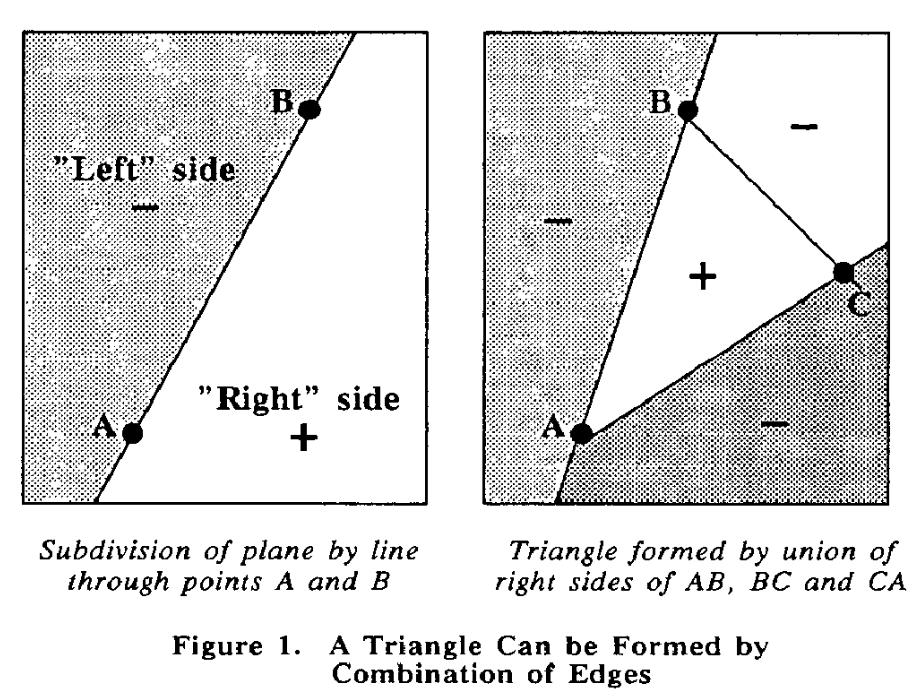
Edge function

Let’s take two points \((X, Y)\) and \((X+dx, Y=dy)\)

Define an edge function:

\[E(x, y) = (x - X)dy - (y - Y)dx\]

[1]

Edge function values

If \(E(x, y)>0\) then \((x, y)\) on the “right” side

If \(E(x, y)<0\) then \((x, y)\) on the “left” side

If \(E(x, y)=0\) then \((x, y)\) on the edge

[1]

Edge function view

[1]

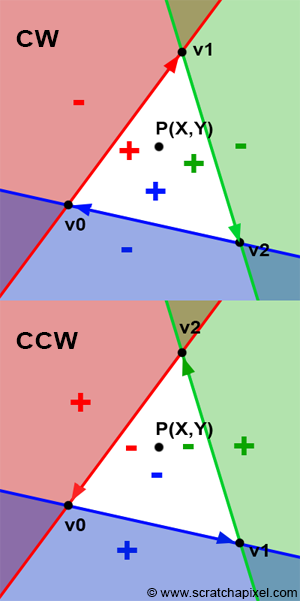
Clockwise vs counter-clockwise

[2]

“Edge functione rasterization” experiment

Deduction phase

• We have a correct wire frame triangles
• We know about the edge function
• How to fill triangles by solid color?
• What about performance?

“Edge function rasterization” experiment

Experiment

Let’s implement it together

“Edge function rasterization” experiment

Reference

“Edge function rasterization” experiment

What is the new knowledge?

• Edge function rasterization is good to fill triangles by solid color
• Clockwise vertex order is required

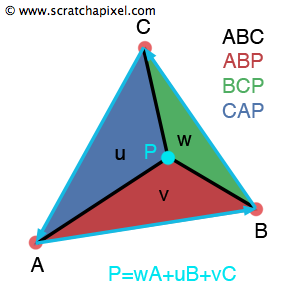
Barycentric coordinates

Let exists \[P=uA+vB+wC\], where \(u+v+w=1\)

[3]

2D cross product cheating

\[(u_1, u_2, 0) \times (v_1, v_2, 0) = (0, 0, u_1v_1-u_2v_1)\]

and compare with

\[E(x, y) = (x - X)dy - (y - Y)dx\]

“Barycentric flavor rasterization” experiment

Deduction phase

• We have a correct wire frame triangles
• We know about the edge function
• We know how to fill with solid color
• How to fill triangles by interpoladed color?
• What about performance?

“Barycentric flavor rasterization” experiment

Experiment

Let’s implement it together

“Barycentric flavor rasterization” experiment

Reference

“Barycentric flavor rasterization” experiment

What is the new knowledge?

• Barycentric flavor rasterization is good if you need interpolate something during rasterization
• Clockwise vertex order is required