Lecture 03: Vertex transformations

Rendering pipeline

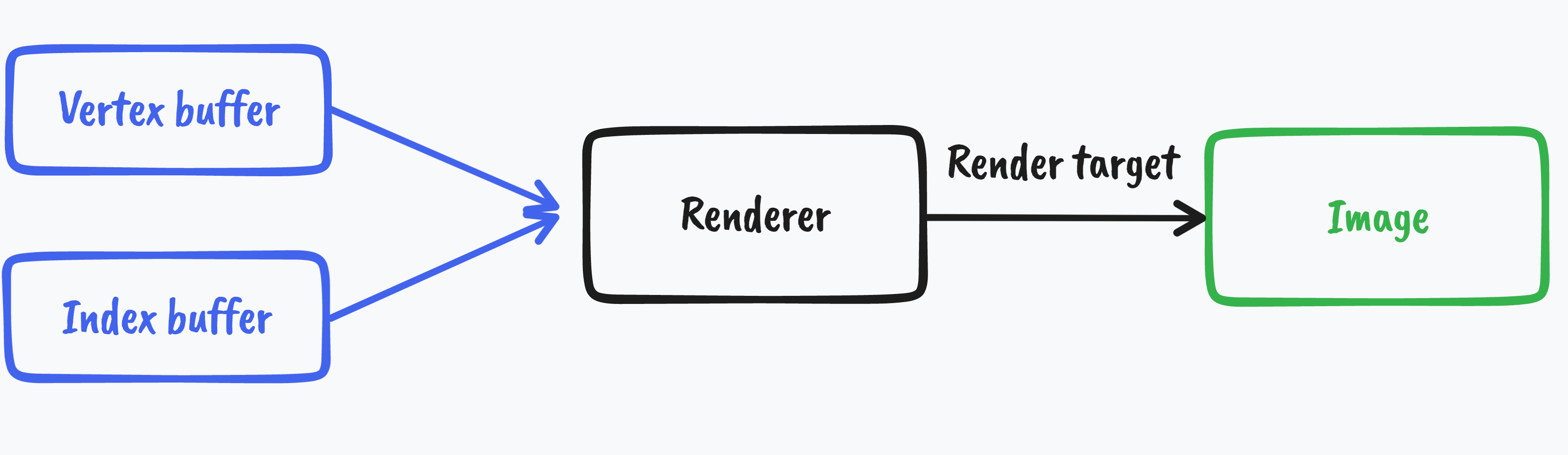
Vertex data

• Vertex position (in cartesian coordinates)
• Vertex normal
• Texture coordinates
• Vertex color (diffuse, specular, ambient)

Vertex position transformation

Goal: find a transformation of the vertex position to a screen position

1. From model space to world space
2. From world space to view space (camera space)
3. From view space to projection space
4. From projection space to clipping space
5. From clipping space to homogeneous screen space
6. From homogeneous screen space to screen space [1]

Spaces

• Model space - coordinate system where the object was created
• World space - where all object located in proper locations
• View space - a space located around camera
• Projection space - a projected camera frustrum to cube space
• Screen space - a space of resulted image [2]

Rendering pipeline: Input-Assembler stage

• Read index and vertex buffers
• Assemble a primitive (triangle)
• Convert cartesian coordinates to homogeneous coordinates [3]

Homogeneous coordinates

Homogeneous coordinates - cartesian coordinates + 1 dimension

\[ (X, Y, Z) => (x, y, z, w) \]

\[ X = x/w, Y = y/w, Z = z/w \] [4]

Transformations in homogeneous coordinates

\[T(\overrightarrow{x}) = A\overrightarrow{x}\]

where \[A = \left[\begin{array}{cccc} x1 & x2 & x3 & x4 \\ y1 & y2 & y3 & y4 \\ z1 & z2 & z3 & z4 \\ w1 & w2 & w3 & w4 \end{array}\right]\] [5]

Rendering pipeline: Vertex shader stage

• Make a vertex transformation from model space to projection space
• Adjust or passthrough rest vertex data
• Graphics programmer should write a code to perform the stage [6]

Vertex shader transformations

Model space -> World space -> View space -> Projection space

Translation in homogeneous coordinates

\(\overrightarrow{tr}\) - vector of translation

\[T = \left[\begin{array}{cccc} 1 & 0 & 0 & tr.x \\ 0 & 1 & 0 & tr.y \\ 0 & 0 & 1 & tr.z \\ 0 & 0 & 0 & 1 \end{array}\right]\] [5]

Scaling in homogeneous coordinates

\(\overrightarrow{scale}\) - vector of scaling

\[S = \left[\begin{array}{cccc} scale.x & 0 & 0 & 0 \\ 0 & scale.y & 0 & 0 \\ 0 & 0 & scale.z & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\] [5]

Rotation around X

\(\alpha\) - angle of rotation around axis X

\[R_x = \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) & 0 \\ 0 & sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\] [5]

Rotation around Y

\(\beta\) - angle of rotation around axis Y

\[R_y = \left[\begin{array}{cccc} cos(\beta) & 0 & sin(\beta) & 0 \\ 0 & 1 & 0 & 0 \\ -sin(\beta) & 0 & cos(\beta) & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\] [5]

Rotation around Z

\(\gamma\) - angle of rotation around axis Z

\[R_z = \left[\begin{array}{cccc} cos(\gamma) & -sin(\gamma) & 0 & 0 \\ sin(\gamma) & cos(\gamma) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\] [5]

World transformations

\[World=TRS\]

First scale, then rotate, then translate

Camera model

• \(\overrightarrow{eye}\) - camera location vector
• \(\overrightarrow{at}\) - camera look-at target
• \(\overrightarrow{up}\) - camera up vector (or world up direction)

Why we need to specify up direction

View transformations

\[ \overrightarrow{z_{axis}} = \frac{\overrightarrow{eye} - \overrightarrow{at}}{||\overrightarrow{eye} - \overrightarrow{at}||} \] \[ \overrightarrow{x_{axis}} = \frac{\overrightarrow{up} \times \overrightarrow{z_{axis}}}{||\overrightarrow{up} \times \overrightarrow{z_{axis}}||}\] \[ \overrightarrow{y_{axis}} = \overrightarrow{z_{axis}} \times \overrightarrow{x_{axis}} \]

View transformations

\[View = \left[\begin{array}{cccc} x_{axis}.x & y_{axis}.x & z_{axis}.x & 0 \\ x_{axis}.y & y_{axis}.y & z_{axis}.y & 0 \\ x_{axis}.z & y_{axis}.z & z_{axis}.z & 0 \\ -\overrightarrow{x_{axis}} \cdot \overrightarrow{eye} & -\overrightarrow{y_{axis}} \cdot \overrightarrow{eye} & -\overrightarrow{z_{axis}} \cdot \overrightarrow{eye} & 1 \end{array}\right]\]

Camera model ideas

Look-at target could be replaced as camera location vector + unit camera direction vector.

Unit direction vector could be set in spherical coordinates.

Projection parameters

• \(fov\) - field of view angle
• \(ar\) - aspect ratio (width to height)
• \(Z_n\) - distance to the near clipping plane along Z axes in camera space
• \(Z_f\) - distance to the far clipping plane along Z axes in camera space

Perspective projection

\[Proj = \left[\begin{array}{cccc} \frac{1}{tan(fov/2)\cdot ar} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(fov/2)} & 0 & 0 \\ 0 & 0 & \frac{Z_f}{Z_n-Z_f} & -1 \\ 0 & 0 & \frac{Z_n\cdot Z_f}{Z_n-Z_f} & 0 \end{array}\right]\]

Vertex shader transformation

\[\vec{X} = Proj \cdot View \cdot World \cdot \vec{x}\]

Dangerous zone

Remember about left-handed and right-handed operations!

Check correctness of each matrix, e.x. in DirectX documentation [1]

Lab: 1.04 Vertex transformation

1. Implement cg::world::camera class
2. Setup an instance of camera cg::world::camera class in cg::renderer::rasterization_renderer
3. Implement vertex_shader lambda for the instance of cg::renderer::rasterizer
4. Add IA and Vertex shader stages to draw method of cg::renderer::rasterizer