Lecture 04: Triangle rasterization

Rendering pipeline

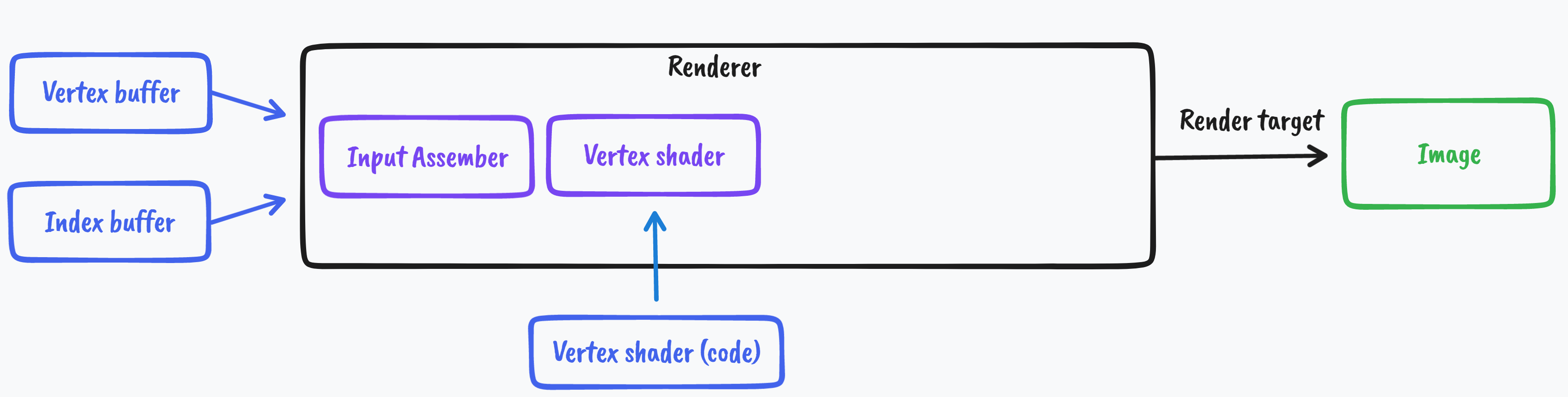
Rasterization

After vertex shader stage we have an NDC coordinates of each vertex of the triangle.

Next steps:

• Convert NDC to screen space coordinates
• Find the triangle bounding rectangle
• Clip the triangle to screen space size
• For each pixel inside the bounding rectangle decide which pixel inside the triangle or not
• For each pixel inside the triangle compute a color with a pixel shader [1]

Convert NDC to screen space coordinates

Could be done in homogeneous coordinates or cartesian

\[M_{ss} = \left[\begin{array}{cccc} width & 0 & 0 & 0 \\ 0 & - height & 0 & 0 \\ 0 & 0 & 1 & 0 \\ x & height + y & 0 & 1 \end{array}\right]\]

where \(x\) and \(y\) are offsets from the screen space \((0, 0)\) [1]

Bounding rectangle

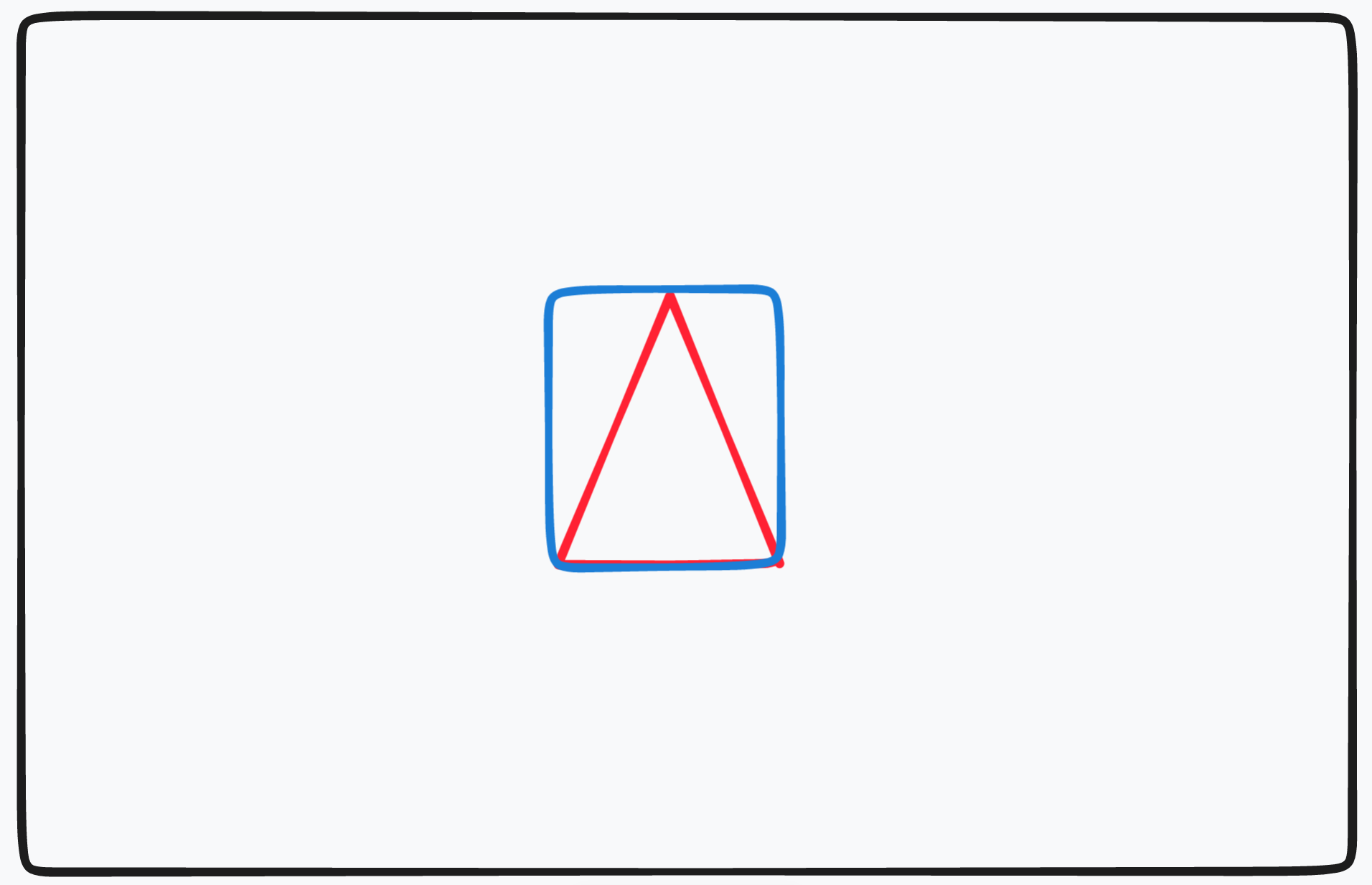
How to find whether the pixel is inside the triangle - Edge function

Let’s take two points \((X, Y)\) and \((X+dx, Y+dy)\) on an edge

Then, define an edge function:

\[E(x, y) = (x - X)dy - (y - Y)dx\]

[2]

Edge function values

If \(E(x, y)>0\) then \((x, y)\) on the “right” side

If \(E(x, y)<0\) then \((x, y)\) on the “left” side

If \(E(x, y)=0\) then \((x, y)\) on the edge

[2]

Edge function view

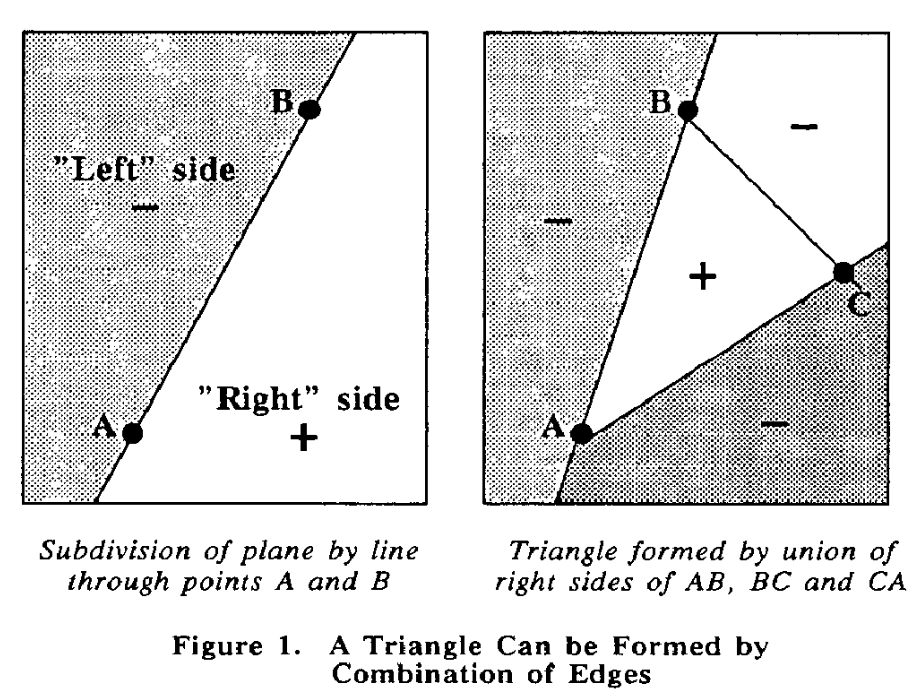[2]

Clockwise vs counter-clockwise

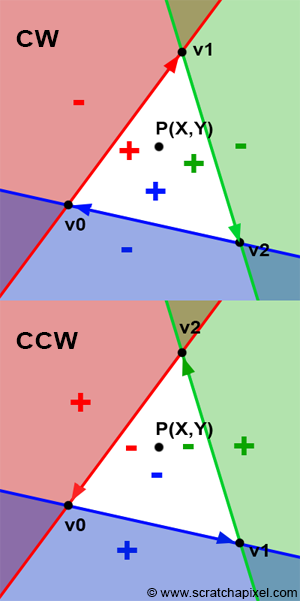[3]

Another meaning of the edge function

Lets compare \[E(x, y) = (x - X)dy - (y - Y)dx\]

and \[(u_1, u_2, 0) \times (v_1, v_2, 0) = (0, 0, u_1v_1-u_2v_1)\]

The edge function value is a twice area of the triangle

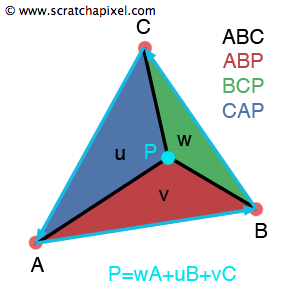
Barycentric coordinates

Let \(u = \frac{S_{CAP}}{S_{ABC}}\), \(v = \frac{S_{BCP}}{S_{ABC}}\), \(w = \frac{S_{ABP}}{S_{ABC}}\)

Therefore, \(u+v+w=1\), and \(P=uA+vB+wC\). The barycentric could be used for attribute interpolation [4]

Pixel shader

Input: interpolated vertex attributes

Output: result pixel color

The pixel shader should be provided by graphics programmer [5]

Lab: Triangle rasterization

1. Implement cg::renderer::rasterizer::edge_function method
2. Implement pixel_shader lambda for the instance of cg::renderer::rasterizer
3. Add Rasterization and Pixel shader stages to draw method of cg::renderer::rasterizer
4. Make sure that you are getting correct image as a result