Lecture #08. Lighting and shadows

Current result vs rasterizer

Rendering equation

\[\scriptsize{L_o(X, \vec{\omega_o}) = L_e(X, \vec{\omega_o}) + \int_S L_i(X, \vec{\omega_i}) f_{X,\vec{n}}(\vec{\omega_i}, \vec{\omega_o}) |\vec{\omega_i} \cdot \vec{n} | d{\omega_i}} \]

where \(X\) is a position on the object or surface,

\(\vec{\omega_o}\) is a direction toward the eye or camera,

\(L_o(X, \vec{\omega_o})\) is all outgoing light from the position,

\(L_e(X, \vec{\omega_o})\) is emitted light [1]

Rendering equation

\[\scriptsize{L_o(X, \vec{\omega_o}) = L_e(X, \vec{\omega_o}) + \int_S L_i(X, \vec{\omega_i}) f_{X,\vec{n}}(\vec{\omega_i}, \vec{\omega_o}) |\vec{\omega_i} \cdot \vec{n} | d{\omega_i}} \]

where \(\vec{n}\) is normal to surface at \(X\) position,

\(S\) is a unit hemisphere among \(\vec{n}\) with center in \(X\),

\(L_i(X, \vec{\omega_i})\) is a light coming from \(\vec{\omega_i}\) direction,

\(f_{X,\vec{n}}(\vec{\omega_i}, \vec{\omega_o})\) is the bidirectional reflectance distribution function (BRDF) [1]

Bidirectional reflectance distribution function

Phong shading

\[\small{L(\vec{P}) = Ka + \sum_{lights}{[Kd\vec{N} \cdot \vec{L} + Ks(\vec{V} \cdot \vec{R})^{Ns}]}}\]

where \(\small{\vec{R} = 2(\vec{N} \cdot \vec{L})\vec{N}−\vec{L}}\) [3]

Lambertian shading

\[L_d = k_dI\max(0, \vec{n}\cdot\vec{l})\]

where \(L_d\) - diffusely reflected light,

\(k_d\) - material’s diffuse coefficient,

\(\vec{n}\) - surface normal,

\(\vec{l}\) - direction toward the light [4]

Lab: 2.03 Lambertian shading

1. Add light information to lights array of ray_tracing_renderer
2. Adjust closest_hit_shader of raytracer to implement Lambertian shading model

Shadow rays idea

Before adding the light source to the final point on the point \(X\), we should cast a ray from the point \(X\) towards the light source. If any object occludes the shadow ray, the point \(X\) is on shadow and the light should not be added the light source

Shadow rays

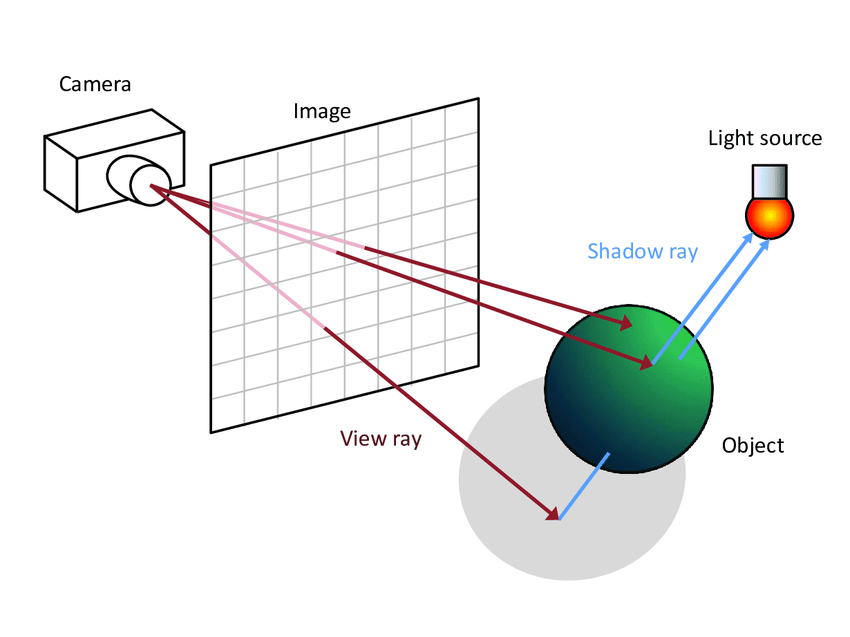
Shadow rays tips

• Intersection with any geometry farther than light source doesn’t occlude the light source. To skip such object cast the ray with \(t_{max}\) less than distance from \(X\) to the light source
• To avoid self-intersection with the triangle owning \(X\), use \(t_{min}\) more than 0
• One intersection is enough to find an occlusion - use an AnyHit shader

Lab: 2.04 Shadow rays

1. Adjust trace_ray method of raytracer to use any_hit_shader
2. Initialize shadow_raytracer in ray_tracing_renderer
3. Define any_hit_shader and miss_shader for shadow_raytracer
4. Adjust closest_hit_shader of raytracer to cast shadows rays and to ignore occluded lights