Lecture 08: Lighting and shadows

Rendering equation

\[\scriptsize{L_o(X, \vec{\omega_o}) = L_e(X, \vec{\omega_o}) + \int_S L_i(X, \vec{\omega_i}) f_{X,\vec{n}}(\vec{\omega_i}, \vec{\omega_o}) |\vec{\omega_i} \cdot \vec{n} | d{\omega_i}} \]

where \(X\) is a position on the object or surface,

\(\vec{\omega_o}\) is a direction toward the eye or camera,

\(L_o(X, \vec{\omega_o})\) is all outgoing light from the position,

\(L_e(X, \vec{\omega_o})\) is emitted light [1]

Rendering equation

\[\scriptsize{L_o(X, \vec{\omega_o}) = L_e(X, \vec{\omega_o}) + \int_S L_i(X, \vec{\omega_i}) f_{X,\vec{n}}(\vec{\omega_i}, \vec{\omega_o}) |\vec{\omega_i} \cdot \vec{n} | d{\omega_i}} \]

where \(\vec{n}\) is normal to surface at \(X\) position,

\(S\) is a unit hemisphere among \(\vec{n}\) with center in \(X\),

\(L_i(X, \vec{\omega_i})\) is a light coming from \(\vec{\omega_i}\) direction,

\(f_{X,\vec{n}}(\vec{\omega_i}, \vec{\omega_o})\) is the bidirectional reflectance distribution function (BRDF) [1]

Bidirectional reflectance distribution function

Phong shading

\[\small{L(\vec{P}) = Ka + \sum_{lights}{[Kd\vec{N} \cdot \vec{L} + Ks(\vec{V} \cdot \vec{R})^{Ns}]}}\]

where \(\small{\vec{R} = 2(\vec{N} \cdot \vec{L})\vec{N}−\vec{L}}\) [3]

Lambertian shading

\[L_d = k_dImax(0, \vec{n}\cdot\vec{l})\]

where \(L_d\) - diffusely reflected light,

\(k_d\) - material’s diffuse coefficient,

\(\vec{n}\) - surface normal,

\(\vec{l}\) - direction toward the light [4]

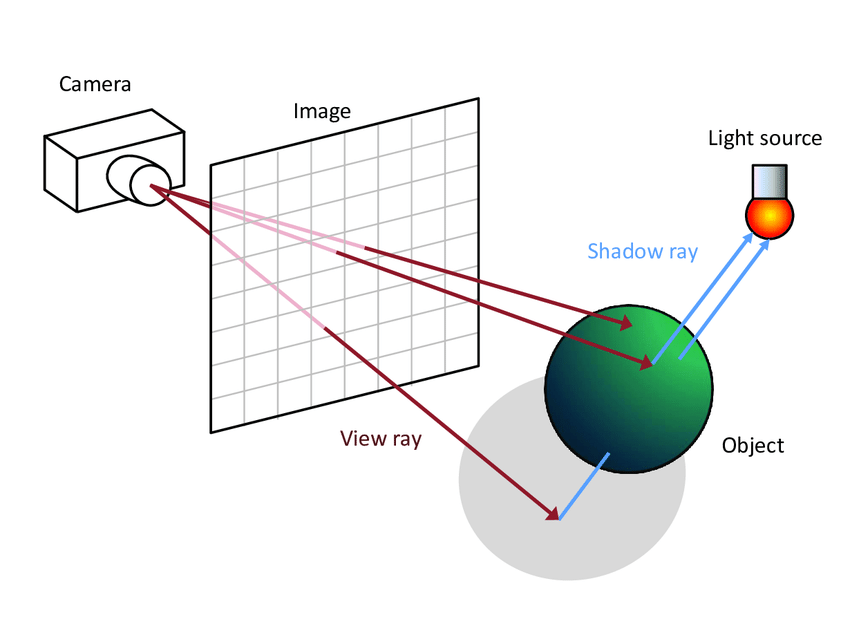
Shadow rays