Lecture 04: Triangle rasterization

Computer graphics in Game development

Ivan Belyavtsev

23.01.2021

Rendering pipeline

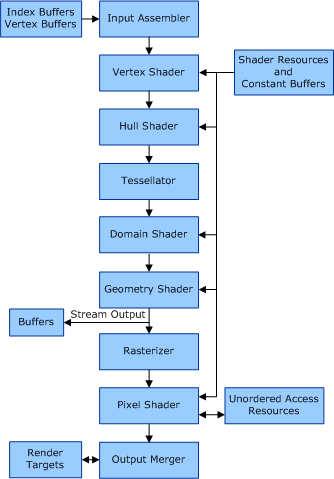
From: https://docs.microsoft.com/en-us/windows-hardware/drivers/display/pipelines-for-direct3d-version-11

Essential of rendering pipeline

Input assembler packs vertices to triangles
Vertex shader performs projections in homogeneous coordinates
Rasterizer decides which pixel will be covered by the triangle and interpolate attributes
Pixel shader produces pixel color based on attributes

Edge function

Let’s take two points \((X, Y)\) and \((X+dx, Y=dy)\)

Define an edge function:

\[E(x, y) = (x - X)dy - (y - Y)dx\]

[1]

Edge function values

If \(E(x, y)>0\) then \((x, y)\) on the “right” side

If \(E(x, y)<0\) then \((x, y)\) on the “left” side

If \(E(x, y)=0\) then \((x, y)\) on the edge

[1]

Edge function view

From: https://www.cs.drexel.edu/~david/Classes/Papers/comp175-06-pineda.pdf [1]

Clockwise vs counter-clockwise

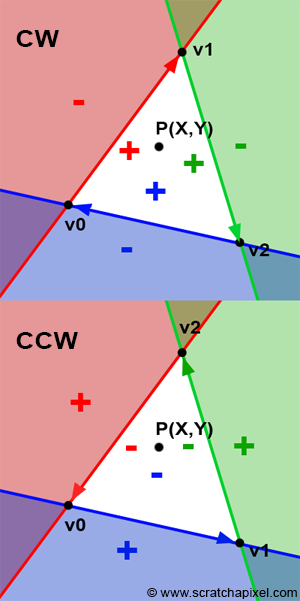From: https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/rasterization-stage [2]

Barycentric coordinates

Let exists \(P=uA+vB+wC\), where \(u+v+w=1\)

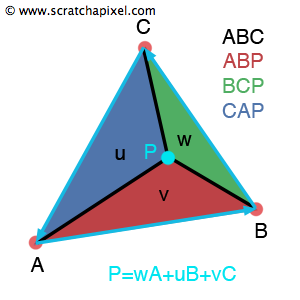From: https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-rendering-a-triangle/barycentric-coordinates [3]

2D cross product cheating

\[(u_1, u_2, 0) \times (v_1, v_2, 0) = (0, 0, u_1v_1-u_2v_1)\]

and compare with

\[E(x, y) = (x - X)dy - (y - Y)dx\]

Lab: Rasterization

References

Pineda J. A parallel algorithm for polygon rasterization // Proceedings of the 15th annual conference on computer graphics and interactive techniques. 1988. P. 17–20.

Rasterization: A practical implementation [Electronic resource]. 2015. URL: https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/rasterization-stage.

Ray tracing: Rendering a triangle [Electronic resource]. 2014. URL: https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-rendering-a-triangle/barycentric-coordinates.